왜 (a | b)가 a - (a & b) + b와 같습니까?
오라클 데이터베이스로 BITO()를 수행하는 방법을 찾고 있었는데 BITO(a,b)를 +b - BITAND(a,b)로 대체하여 대신 BITOR()를 사용하자는 제안을 발견했습니다.
저는 그것을 손으로 몇 번 테스트했고 제가 생각할 수 있는 모든 이진수에 효과가 있다는 것을 확인했지만, 왜 이것이 정확한지에 대한 빠른 수학적 증거를 생각해 낼 수 없습니다.
누가 좀 가르쳐 주시겠어요?
A & B는 A와 B 모두에서 켜지는 비트 집합입니다.A - (A & B)는 A에만 있는 모든 비트를 남깁니다.여기에 B를 더하면 A에 있는 모든 비트나 B에 있는 비트를 얻을 수 있습니다.
A와 B를 단순하게 추가하는 것은 둘 다 1비트를 가지고 있기 때문에 작동하지 않을 것입니다.A와 B에 공통된 비트를 먼저 제거하면 (A-(A&B))가 B와 공통된 비트가 없다는 것을 알 수 있으므로, 이들을 함께 추가하면 캐리가 생성되지 않습니다.
의 이진수가 해 보세요: 두 의 개 이 가 정 니 합 다 고 있 다 가 진 수 니 다 합 : 가 ▁imagine ▁numbers 정a그리고.b그리고 이 숫자들이 동시에 같은 비트에 1을 갖는 일이 결코 없다고 하자, 즉, 만약 그렇다면.a어느 정도는 1개를 가지고 있습니다.b해당 비트에는 항상 0이 있습니다.그리고 다른 방향으로, 만약에.b어느 정도는 1개를 가지고 있습니다, 그럼.a해당 비트에는 항상 0이 있습니다.를 들어, .
a = 00100011
b = 11000100
은 이다음같예다니입의 입니다.a그리고.b상기 조건을 만족하는이 경우에는 쉽게 알 수 있습니다.a | b와 정확히 같을 것입니다.a + b.
a | b = 11100111
a + b = 11100111
이제 우리의 조건을 위반하는 두 개의 숫자를 보겠습니다. 즉, 두 개의 숫자는 어떤 공통 비트에서 적어도 하나의 1을 가집니다.
a = 00100111
b = 11000100
아이즈a | b과 같은a + b이 경우에?아니요.
a | b = 11100111
a + b = 11101011
왜 그들은 다릅니까?그들은 다르기 때문에 우리가+두 숫자 모두에 1이 있는 비트는 소위 캐리를 생성합니다. 결과 비트는 0이고 1은 왼쪽 다음 비트로 이동합니다.1 + 1 = 10.작동|소품이없습다니지▁has없.1 | 1다시 1입니다.
은 이는사차의미다니합이를의이rence의 합니다.a | b그리고.a + b숫자에 공통 비트가 하나 이상 있는 경우에만 발생합니다.의 숫자를 , 이은 "두 번하는데, 은 우가공과비 1개 2의숫합할때두를자번추리은가며되이고캐하생리를성다니들망트칩유을성사사이의이비두개트는의비통통공트서에,▁carry▁▁between▁a두▁similar▁with▁get,tw다▁in▁numbers니ice칩과▁bits▁these▁ruins▁common▁two▁bits개▁1망▁which유을성사▁sum▁and의사▁produce이▁common우"▁added▁"비▁we리,가트개두의이는a | b그리고.a + b.
, 이제 보요세이를 보세요.a & b.무인가가 입니까?a & b계산? a & b두 비트 모두에서 1을 갖는 숫자를 생성합니다.a그리고.b1을 가지다가장 최근의 예에서
a = 00100111
b = 11000100
a & b = 00000100
위에서 본 것처럼, 이것들은 정확히 다음과 같은 것들을 만듭니다.a + b와 다른a | b더 원 인a & b운반이 발생하는 모든 위치를 나타냅니다.
이제, 우리가 할 때.a - (a & b)우리는 모든 "유해한" 비트를 효과적으로 제거(제거)합니다.a그리고 그런 부분들만.
a - (a & b) = 00100011
숫자a - (a & b)그리고.b공통된 1비트가 없습니다. 즉, 우리가 추가하면a - (a & b)그리고.b우리는 캐리와 마주치지 않을 것이고, 생각해보면, 우리는 마치 방금 한 것과 같은 결과로 끝나야 합니다.a | b
a - (a & b) + b = 11100111
A&B = C 여기서 C에 설정된 비트는 A와 B 모두에 설정된 비트입니다.
A-C = D 또는 B-C = E는 이러한 공통 비트만 0으로 설정합니다.1-1=0이므로 전달 효과가 없습니다.
D+B 또는 E+A는 이전에 A&B를 뺀 것이기 때문에 D 또는 E에서 일반적으로 설정된 모든 비트를 지웠기 때문에 캐리가 없다는 점을 제외하면 A+B와 유사합니다.
최종 결과는 A-A&B+B 또는 B-A&B+A가 A|B와 동등하다는 것입니다.
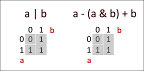
여전히 혼란스럽다면 다음 표를 참조하십시오.
A | B | OR | B | & A | B | - A | B | +---+---+---- ---+---+--- ---+---+--- ---+---+---0 | 0 | 0 0 | 0 | 0 0 | 0 | 0 0 | 0 | 00 | 1 | 1 0 | 1 | 0 0 | 1 | 0-1 0 | 1 | 11 | 0 | 1 1 | 0 | 0 1 | 0 | 1 1 | 0 | 11 | 1 | 1 1 | 1 | 1 1 | 1 | 0 1 | 1 | 1+1
+ 및 - 연산의 캐리 행에 주목하십시오. A-(A&B) 세트가 모두 A의 비트이고 B의 비트가 A의 1에서 0이기 때문에 이러한 행을 피합니다. B에서 이를 다시 추가하면 A 또는 B 중 하나에 1이 있지만 둘 다 0이 아닌 다른 경우에도 마찬가지입니다. 따라서 OR 진실 테이블과 A-(A&B)+B 진실 테이블이 동일합니다.
또 다른 안목으로 보면 A+B가 A|B와 거의 비슷하다는 것을 알 수 있습니다. 맨 아래 행을 A&B가 분리하면 A-A&B는 + 표에서 분리된 케이스를 두 줄 위로 이동하고 (A-A&B)+B는 A|B와 동일해집니다.
당신이 이것을 A+B-(A&B)로 통근할 수 있지만, 저는 오버플로가 발생할 수 있다는 것이 두려웠지만, 그것은 정당하지 않은 것 같습니다.
#include <stdio.h>
int main(){ unsigned int a=0xC0000000, b=0xA0000000;
printf("%x %x %x %x\n",a, b, a|b, a&b);
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); }
c0000000 a0000000 e0000000 80000000
60000000 40000000 e0000000 e0000000
편집: 그래서 저는 답이 오기 전에 이것을 썼습니다. 그리고 나서 제 집 연결에 2시간의 다운타임이 있었습니다. 그리고 마침내 저는 그것을 게시할 수 있었습니다. 그 후에야 그것이 두 번이나 제대로 대답되었다는 것을 알아차렸습니다.개인적으로 저는 비트적인 작업을 해결하기 위해 진실표를 참조하는 것을 선호하기 때문에 누군가에게 도움이 될 경우를 대비해 남겨두겠습니다.
언급URL : https://stackoverflow.com/questions/1604258/why-is-a-b-equivalent-to-a-a-b-b
'programing' 카테고리의 다른 글
| Vim에서 Python 코드 실행 중 (0) | 2023.07.18 |
|---|---|
| 플라스크에서 매 시간 실행되도록 함수를 예약하는 방법은 무엇입니까? (0) | 2023.07.18 |
| 장고 1.7 - 변경 사항을 감지하지 않는 마이그레이션 수행 (0) | 2023.07.18 |
| SQL Server 에이전트 작업 - 존재한 후 삭제하시겠습니까? (0) | 2023.07.18 |
| 개체 'sysobjects', 데이터베이스 'mssqlssystem resource', 스키마 'sys'에 대한 SELECT 권한이 거부되었습니다. (0) | 2023.07.13 |